А рельсы-то, как водится, у горизонта сходятся

Филателист Александр Платонов из Тюмени продолжает знакомить нас с великими математиками, которые перевернули наше сознание. 

* * *

В 1956 году в СССР была выпущена почтовая марка к 100-летию со дня смерти русского математика Николая Ивановича Лобачевского.

Марка выполнена на основе его прижизненного портрета, написанного казанским художником Л.Д. Крюковым.

Для почтового конверта и почтовой карточки с изображением Лобачевского использовался другой портрет работы неизвестного художника, возможно, Л.Д. Крюкова.

Буйный студент, великий ректор и создатель новой геометрии – таким запомнился Лобачевский потомкам.

Обложка книги по геометрии

Родился ученый в Нижнем Новгороде в 1792 году. Первое образование получил в Казанской гимназии. В то время это было единственное учебное заведение подобного типа в восточной части России. В 1807 году был зачислен студентом, в недавно открытый Казанский университет.

Имея бойкий и неугомонный нрав и темперамент, с репутацией упрямца и бунтаря, он шаг за шагом быстро продвинулся на научно-педагогическом поприще: магистр – адъюнкт (доцент) – экстраординарный профессор – декан – ординарный профессор. В 1827 году в возрасте 34 лет он становится ректором Казанского университета, пробыв на этой должности 20 лет, сделав университет одним из ведущих учебных заведений России.

Казанский университет в 1830-е годы

А вот имя Лобачевского носит другой, Нижегородский университет, по месту рождения ученого.

При создании университета в Казань было приглашено много европейских преподавателей. Среди них был и профессор Иоганн Бартельс – учитель Карла Фридриха Гаусса – великого немецкого математика, астронома и физика. Это не в малой степени сказалось на научной деятельности и самого Лобачевского как математика.

Основоположником геометрии как науки считается древнегреческий ученый Евклид, который создал свою математическую школу в Афинах. На картине Рафаэля Санчи на марке республики Кампучия запечатлен Евклид с циркулем в руках в окружении своих учеников.

Нам со школьной скамьи хорошо знакома геометрия Евклида. Здесь мы узнаем о свойствах плоских геометрических фигур: длине окружности и площади круга, свойствах треугольника, прямоугольника, трапеции. У треугольника сумма внутренних углов равна 180, а у четырехугольника – 360 градусов. Если на тетрадном листе поставить, допустим, две точки на разном расстоянии от края, то через каждую из них можно провести только одну линию, параллельно краю листа. Появятся две линии, которые нигде не пересекаются. Это одна из аксиом геометрии Евклида, геометрии на плоскости.

Лобачевский является основоположником новой, неевклидовой геометрии. За основу взята не плоскость, а криволинейная поверхность. На почтовом конверте 1992 года эта поверхность стилистически показана на оригинальной марке в виде гиперболоида.

Объяснять математически, почему именно был выбран гиперболоид, а не что-то другое, в рамках этой статьи этой, думаю, будет неправильно. Отвечу вопросом на вопрос: “А почему инженер Гарин изобрел именно гиперболоид, а не эллипсоид или параболоид, скажем?”.

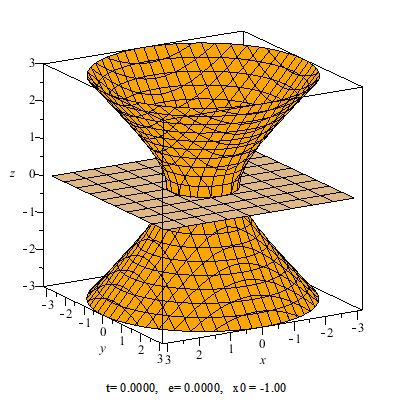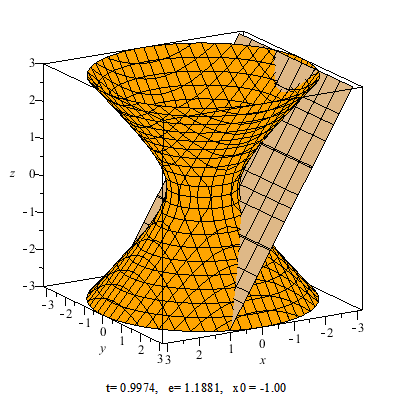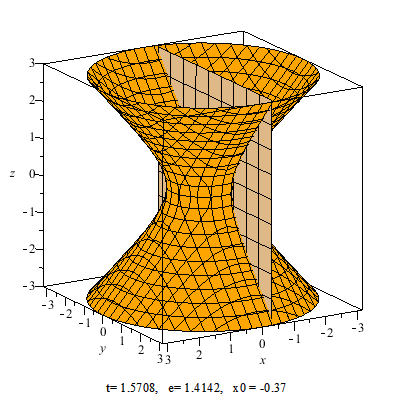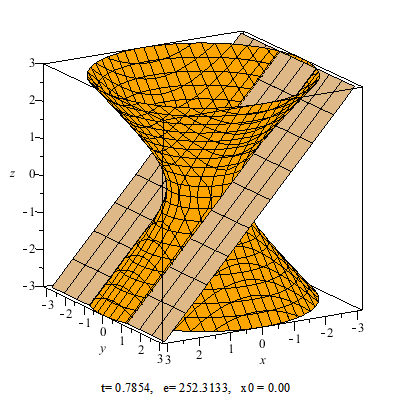
Стилистически слово гипербола означает то, что что-то увеличивается, усиливается. К гиперболоиду человек пришел без всякой математики, исходя из своего практического опыта, получив множество шишек и ушибов. Посмотрите на форму седла. Его поверхность и есть поверхность гиперболоида. Эта форма усиливает наши способности бороться с самой могущественной силой природы – гравитацией.

Следующая почтовая карточка с оригинальной маркой показывает, как выглядит геометрия на искривленной поверхности.

Через точку уже можно провести несколько параллельных прямых, и они пересекаются в этой точке. Треугольник искривляется, стороны становятся длиннее, уменьшается площадь. Сумма углов тоже меньше 180 градусов.

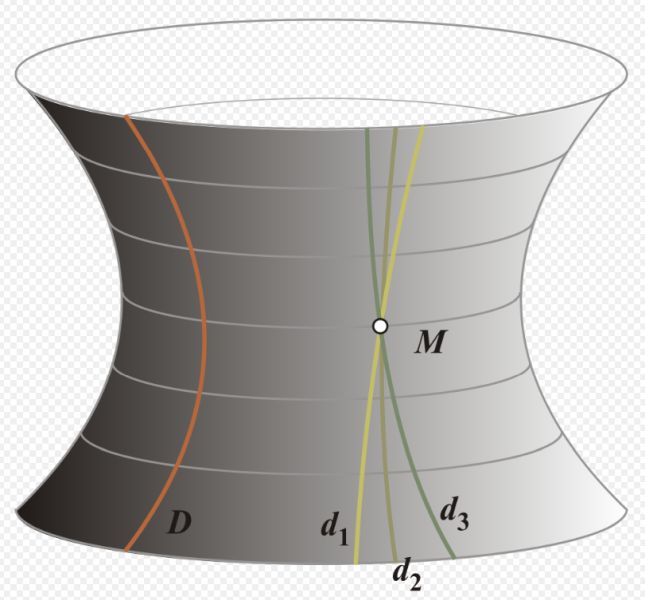
Геометрия Лобачевского – это, возможно, геометрия будущего. Уже в ХХ веке появилась теория об искривлении пространства под действием силы гравитации. Гравитация способна и на отклонение световых лучей. И именно для таких случаев можно будет применять геометрию искривленных пространств.

А пока только машинист поезда видит, как где-то вдали у горизонта пересекаются параллельные рельсы. И чем быстрее он к этой точке пересечения приближается, тем быстрее она убегает. Но надежда достичь цели не угасает, и в следующий раз все повториться вновь.

Последняя работа Лобачевского была записана под его диктовку, так как ученый полностью ослеп.

Источник:

1. Васильев А.В. Николай Иванович Лобачевский, 1792–1856 – М.: Наука, 1992. – 229 с.

2. Фото из свободного доступа. Яндекс. Картинки.

А. Платонов, г. Тюмень